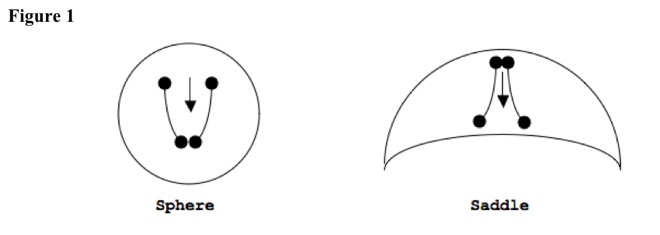
Space-time surfaces and hypersurfaces have a path {geodesic} between two space-time points (events) that has shortest separation {space-time separation}. For no-curvature space-times (planes and hyperplanes), geodesics are straight lines. For no-curvature space-times, separation has shortest distance and shortest time. On spheres and saddles, shortest space distance between two points is great-circle arc. See Figure 1.
spheres
Convex, positive-curvature space-times include spherical surfaces, which have two dimensions, have centers, and have same constant curvature for both coordinates. Starting from nearby points, parallel geodesics converge. Geodesics have shortest-distance and longest-time trajectory.
saddles
Concave, negative-curvature space-times include saddle surfaces, which have two dimensions and have no center or two centers. Coordinates have constant opposite curvature. Starting from nearby points, parallel geodesics diverge. Geodesics have longest-distance and shortest-time trajectory.
geodesics
Experiments show that particles and objects always travel at light speed through space-time, along shortest-separation trajectory (geodesic) between two space-time points, whether or not matter and/or energy are present. Masses free fall along space-time geodesics. Observers and objects traveling along geodesics feel no tidal forces.
object mass
All objects and particles follow the same geodesics. Because inertial mass and gravitational mass are the same, object mass does not affect trajectory. Gravity is not a force but a space-time curvature field.

Physical Sciences>Physics>Relativity>General Relativity>Curvature>Geodesics
5-Physics-Relativity-General Relativity-Curvature-Geodesics
Outline of Knowledge Database Home Page
Description of Outline of Knowledge Database
Date Modified: 2022.0224