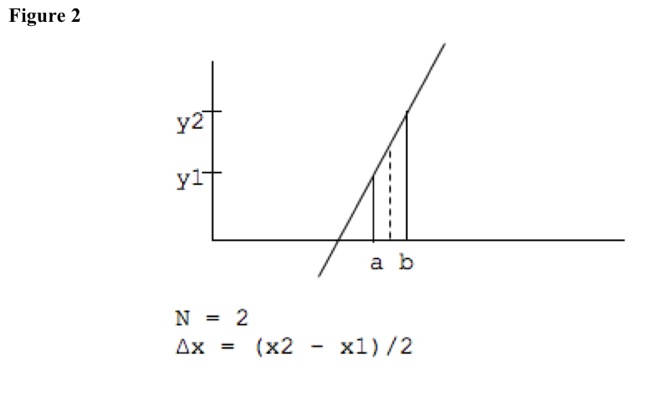
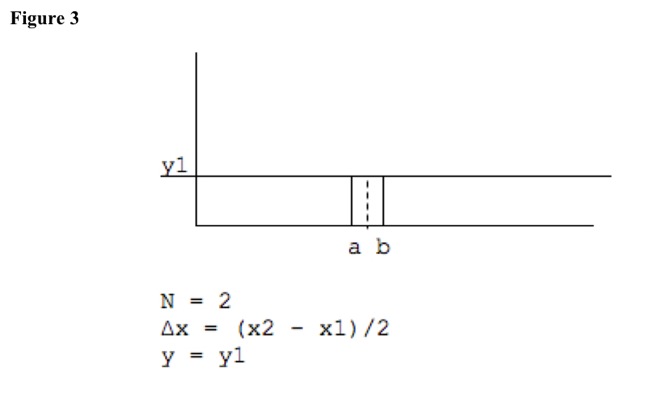
For smoothly changing continuous functions {integrand}, with y-axis range and x-axis domain, you can calculate area between curve and x-axis {integral} {first integral} {integration, calculus}, from lower domain value {lower limit} to higher domain value {upper limit}. For example, you can calculate enclosed-surface area and volume.
summation
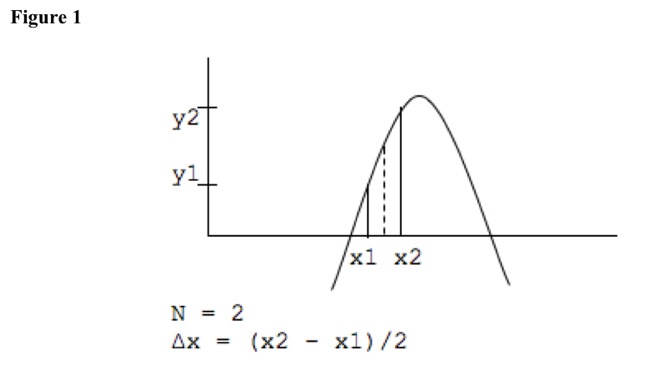
See Figure 1. Domain goes continuously from lower value x1 to higher value x2, while range goes continuously from lower value y1 to higher value y2. Length x2 - x1 can divide into number N of intervals with equal widths (x2 - x1)/N.
In Figure 1, dashed line divides x2 - x1 interval into two intervals, each with width (x2 - x1)/2, because N = 2.
Range at left of each small interval is f(x1 + (ni - 1) * (x2 - x1)/N), for ith interval. For i = 1, it is f(x1). For i = 2, it is f(x1 + (x2 - x1)/2). Range halfway between left and right of each small interval is f(x1 + (ni - 1/2) * (x2 - x1)/N). For i = 1, it is f(x1 + -(1/2) * (x2 - x1)/2). For i = 2, it is f(x1 + (3/2) * (x2 - x1)/2). Range at right of each small interval is f(x1 + ni * (x2 - x1)/N). For i = 1, it is f(x1 + (x2 - x1)/2). For i = 2, it is f(x1 + 2 * (x2 - x1)/2). Product of range and interval width is rectangular area. For example, using left of each small interval, (f(x1 + (ni - 1) * (x2 - x1)/N)) * (x2 - x1)/N, for ith interval. For i = 1, it is f(x1) * (x2 - x1)/2. For i = 2, it is (f(x1 + (x2 - x1)/2)) * (x2 - x1)/2. Sum of all interval areas approximates total area between curve and x-axis, between domain values. As interval number increases, widths decrease, and area sum approaches true area.
interval position
The three different ways of taking interval range do not matter, because total area is same. For example, using right of each small interval, (f(x1 + ni * (x2 - x1)/N)) * (x2 - x1)/N, for ith interval. For i = 1, it is (f(x1 + (x2 - x1))/2) * (x2 - x1)/2. For i = 2, it is f(x1) * (x2 - x1)/2. Total area is the same.
number of intervals
Number of intervals does not matter. Use function f(x) = x^2, as in parabola. Interval is x1 = 0 to x2 = b. Number of subintervals is N = 3. (x2 - x1)/N = b/3. If f(x) is at midpoint of each interval, sum from x1 = 0 to x2 = b of f(x1 + (ni - 1/2) * (x2 - x1)/N) * (x2 - x1)/N is ((b/6)^2 + (b/2)^2 + ((5 * b)/6)^2) * (b/3), which is (b^3)/3. If function f(x) = x^2, x1 = 0, x2 = b, and N = 6, sum from x1 = 0 to x2 = b is ((b/12)^2 + ((3 * b)/12)^2 + ((5 * b)/12)^2 + ((7 * b)/12)^2 + ((9 * b)/12)^2 + ((11 * b)/12)^2) * (b/6), which is (b^3)/3. Therefore, results for different numbers of intervals are the same.
line
If f(x) = x, function is line. See Figure 2. Sum from x1 = a to x2 = b with N = 1 of f(x1 + (ni - 1/2) * (x2 - x1)/N) * (x2 - x1)/N is ((b + a)/2) * (b - a), which is area of trapezoid of base b - a and heights a and b.
constant
If f(x) = C, function is constant. See Figure 3. Sum from x = b to x = a with N = 1 of f(x1 + (ni - 1/2) * (x2 - x1)/N) * (x2 - x1)/N is C * (b - a), which is area of rectangle with height C and length b - a.
definite integral
Given function f(x) and interval (b - a), you can calculate integral from x = a to x = b of f(x) * dx {definite integral}. Domain-value variable dx {dummy variable} {variable of integration} does not appear in definite-integral result, because domain values over interval replace it.
indefinite integral
Without using interval, formula or other method can calculate integral {indefinite integral} {anti-differential} {antiderivative} {antiderived function}. Antiderivatives are functions from which original function can derive by differentiation.
Because derivatives of constants equal zero, function antiderivatives differ by a constant {constant of integration}. Knowing original-function domain and range allows calculating constant.

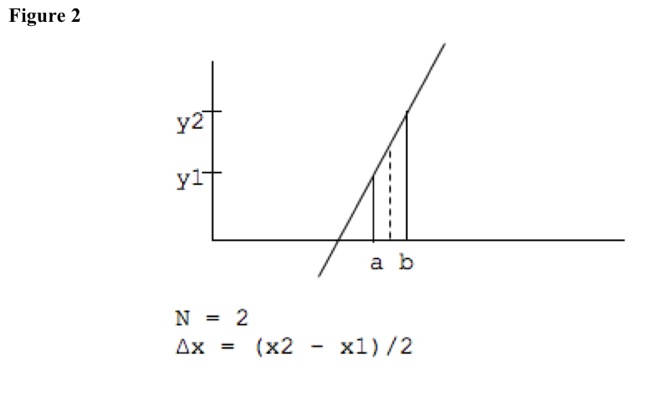
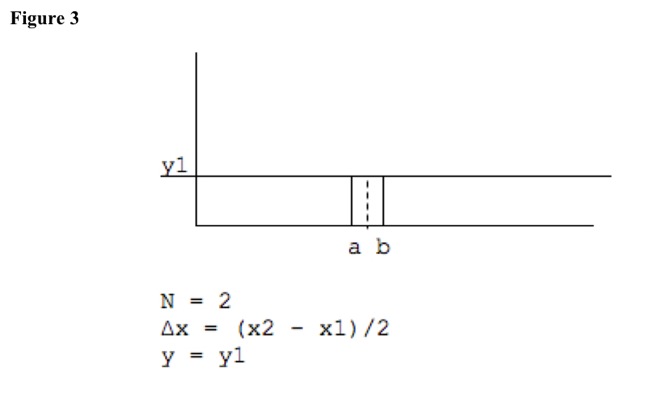
Mathematical Sciences>Calculus>Integration
Outline of Knowledge Database Home Page
Description of Outline of Knowledge Database
Date Modified: 2022.0224